实现目标:
- 分析Butler矩阵与傅里叶变换直接的关系
一. 输入与输出之间的计算
以8×8的接收阵角度为例,输入用$x_1$,…,$x_8$来表示, 输入用$y_1$,…,$y_8$来表示,如下图。
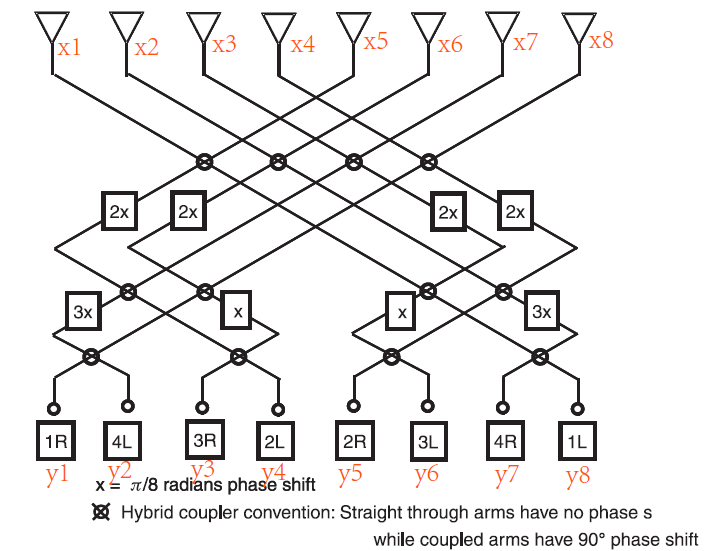
下面来分析如何从输入的$x$得出输出$y$。图中的耦合器在其直连通道上信号不产生相移,而在
其交叉通道上信号具有90°的相移,90°的相移相当于-4x (x=$\pi/8$)。
$$\begin{aligned}
y_8=&x_1+e^{j(3x-4x)}x_2+e^{j(2x-4x)}x_3+e^{j(2x-4x+3x-4x)}x_4+e^{j(-4x)}x_5 \\
&+e^{j(-4x+3x-4x)}x_6+e^{j(-4x+2x-4x)}x_7+e^{j(-4x+2x-4x+3x-4x)}x_8
\end{aligned}$$
…
$$y_8=x_1+e^{j(-x)}x_2+e^{j(-2x)}x_3+e^{j(-3x)}x_4+e^{j(-4x)}x_5+e^{j(-5x)}x_6+e^{j(-6x)}x_7+e^{j(-7x)}x_8$$
$$y_7=e^{j-4x}x_1+e^{j(3x)}x_2+e^{j(-6x)}x_3+e^{j(x)}x_4+e^{j(-8x)}x_5+e^{j(-x)}x_6+e^{j(-10x)}x_7+e^{j(-3x)}x_8$$
…
$$\begin{equation} \begin{bmatrix} y_1\\ y_2\\y_3\\y_4\\y_5\\y_6\\y_7\\y_8\end{bmatrix} =\begin{bmatrix} e^{j(-7x)} & e^{j(-6x)} & e^{j(-5x)} & e^{j(-4x)} & e^{j(-3x)} & e^{j(-2x)} & e^{j(-x)} & e^{0} \\ e^{j(-3x)} & e^{j(-10x)} & e^{j(-x)} & e^{j(-8x)} & e^{j(x)} & e^{j(-6x)} & e^{j(3x)} & e^{j(-4x)} \\ e^{j(-6x)} & e^{j(-x)} & e^{j(-12x)} & e^{j(-7x)} & e^{j(-2x)} & e^{j(3x)} & e^{j(-8x)} & e^{j(-3x)} \\ e^{j(-2x)} & e^{j(-5x)} & e^{j(-8x)} & e^{j(-11x)} & e^{j(2x)} & e^{j(-x)} & e^{j(-4x)} & e^{j(-7x)} \\ e^{j(-7x)} & e^{j(-4x)} & e^{j(-x)} & e^{j(2x)} & e^{j(-11x)} & e^{j(-8x)} & e^{j(-5x)} & e^{j(-2x)} \\ e^{j(-3x)} & e^{j(-8x)} & e^{j(3x)} & e^{j(-2x)} & e^{j(-7x)} & e^{j(-12x)} & e^{j(-x)} & e^{j(-6x)} \\ e^{j(-4x)} & e^{j(3x)} & e^{j(-6x)} & e^{j(x)} & e^{j(-8x)} & e^{j(-x)} & e^{j(-10x)} & e^{j(-3x)} \\ e^{0} & e^{j(-x)} & e^{j(-2x)} & e^{j(-3x)} & e^{j(-4x)} & e^{j(-5x)} & e^{j(-6x)} & e^{j(-7x)} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\x_3\\x_4\\x_5\\x_6\\x_7\\x_8\end{bmatrix} \end{equation}$$将$x=\pi/8$带入上式可得
$$\begin{equation}
\begin{bmatrix} y_1\\ y_2\\y_3\\y_4\\y_5\\y_6\\y_7\\y_8\end{bmatrix}
=\begin{bmatrix}
e^{j(-7\pi/8)} & e^{j(-6\pi/8)} & e^{j(-5\pi/8)} & e^{j(-4\pi/8)} & e^{j(-3\pi/8)} & e^{j(-2\pi/8)} & e^{j(-\pi/8)} & e^{0} \\
e^{j(-3\pi/8)} & e^{j(-10\pi/8)} & e^{j(-\pi/8)} & e^{j(-8\pi/8)} & e^{j(\pi/8)} & e^{j(-6\pi/8)} & e^{j(3\pi/8)} & e^{j(-4\pi/8)} \\
e^{j(-6\pi/8)} & e^{j(-\pi/8)} & e^{j(-12\pi/8)} & e^{j(-7\pi/8)} & e^{j(-2\pi/8)} & e^{j(3\pi/8)} & e^{j(-8\pi/8)} & e^{j(-3\pi/8)} \\
e^{j(-2\pi/8)} & e^{j(-5\pi/8)} & e^{j(-8\pi/8)} & e^{j(-11\pi/8)} & e^{j(2\pi/8)} & e^{j(-\pi/8)} & e^{j(-4\pi/8)} & e^{j(-7\pi/8)} \\
e^{j(-7\pi/8)} & e^{j(-4\pi/8)} & e^{j(-\pi/8)} & e^{j(2\pi/8)} & e^{j(-11\pi/8)} & e^{j(-8\pi/8)} & e^{j(-5\pi/8)} & e^{j(-2\pi/8)} \\
e^{j(-3\pi/8)} & e^{j(-8\pi/8)} & e^{j(3\pi/8)} & e^{j(-2\pi/8)} & e^{j(-7\pi/8)} & e^{j(-12\pi/8)} & e^{j(-\pi/8)} & e^{j(-6\pi/8)} \\
e^{j(-4\pi/8)} & e^{j(3\pi/8)} & e^{j(-6\pi/8)} & e^{j(\pi/8)} & e^{j(-8\pi/8)} & e^{j(-\pi/8)} & e^{j(-10\pi/8)} & e^{j(-3\pi/8)} \\
e^{0} & e^{j(-\pi/8)} & e^{j(-2\pi/8)} & e^{j(-3\pi/8)} & e^{j(-4\pi/8)} & e^{j(-5\pi/8)} & e^{j(-6\pi/8)} & e^{j(-7\pi/8)}
\end{bmatrix}
\begin{bmatrix} x_1\\ x_2\\x_3\\x_4\\x_5\\x_6\\x_7\\x_8\end{bmatrix}
\end{equation}$$
对于$y_1$的输出,相邻阵元加权之间的相位差为$\pi/8$,
对于$y_2$的输出,相邻阵元加权之间的相位差为$-7\pi/8$,
对于$y_3$的输出,相邻阵元加权之间的相位差为$5\pi/8$,
对于$y_4$的输出,相邻阵元加权之间的相位差为$-3\pi/8$,
对于$y_5$的输出,相邻阵元加权之间的相位差为$3\pi/8$,
对于$y_6$的输出,相邻阵元加权之间的相位差为$-5\pi/8$,
对于$y_7$的输出,相邻阵元加权之间的相位差为$7\pi/8$,
对于$y_8$的输出,相邻阵元加权之间的相位差为$-\pi/8$。